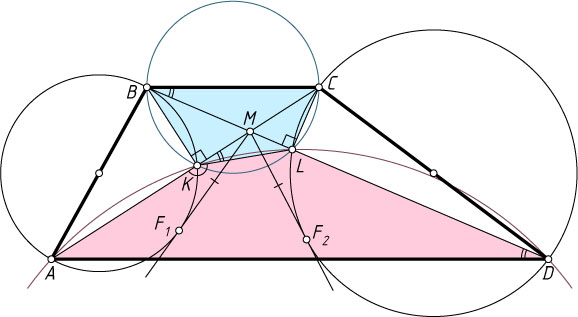
789. На боковых сторонах трапеции как на диаметрах построены окружности. Докажите, что все четыре касательные, проведённые к окружностям из точки пересечения диагоналей, равны между собой (если эта точка лежит вне окружностей).
Указание. Примените теорему о касательной и секущей.
Решение. Пусть AB
и CD
— боковые стороны трапеции ABCD
, M
— точка пересечения диагоналей AC
и BD
, K
— точка пересечения диагонали AC
с окружностью, построенной на боковой стороне AB
как на диаметре, а L
— точка пересечения диагонали BD
со второй окружностью.
Тогда \angle BKC=\angle BLC=90^{\circ}
. Поэтому четырёхугольник BKLC
— вписанный. Следовательно,
\angle CKL=\angle CBL=\angle ADB,~\angle AKL=180^{\circ}-\angle CKL=180^{\circ}-\angle ADL.
Поэтому четырёхугольник AKLD
— также вписанный.
Пусть F_{1}
и F_{2}
— точки касания первой и второй окружностей с касательными, проведёнными из точки M
. Тогда
MF^{2}_{1}=MK\cdot AM=ML\cdot MD=MF^{2}_{2}.
Следовательно, MF_{1}=MF_{2}
. Остальное аналогично.
Автор: Маркелов С. В.
Источник: Турнир городов. — 1994-1995, XVI, весенний тур, старшие классы, основной вариант
Источник: Московская математическая олимпиада. — 1995, LVIII, 10 класс
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 3, с. 28
