792. В треугольнике ABC
перпендикуляр, проходящий через середину стороны AB
, пересекает прямую AC
в точке M
, а перпендикуляр, проходящий через середину стороны AC
, пересекает прямую AB
в точке N
. Известно, что MN=BC
и прямая MN
перпендикулярна прямой BC
. Найдите углы треугольника ABC
.
Ответ. \angle A=60^{\circ}
, \angle B=15^{\circ}
, \angle C=105^{\circ}
или \angle A=60^{\circ}
, \angle B=105^{\circ}
, \angle C=15^{\circ}
.
Указание. Пусть D
и E
середины AB
и AC
. Около четырёхугольника EMDN
можно описать окружность (MN
— её диаметр).
Решение. Пусть BC=a
; D
и E
— середины AB
и AC
.
Точки E
, M
, D
и N
лежат на окружности с диаметром MN
(так как \angle MEN=\angle MDN=90^{\circ}
), MN=a
, ED=\frac{a}{2}
(средняя линия треугольника ABC
). Тогда DE=MN\sin\angle DME
. Следовательно,
\sin\angle DME=\frac{DE}{MN}=\frac{\frac{a}{2}}{a}=\frac{1}{2}.
Тогда либо \angle DME=30^{\circ}
, либо \angle DME=150^{\circ}
.
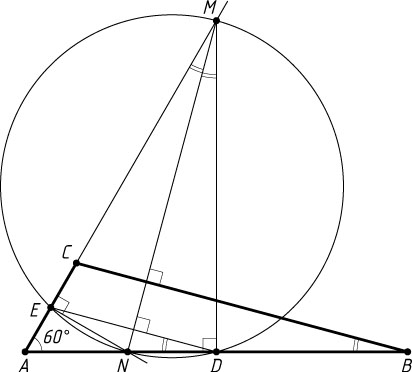
Пусть \angle DME=30^{\circ}
(рис. 1). Тогда
\angle BAC=\angle MAD=90^{\circ}-\angle EMD=60^{\circ}.
Вписанные углы EDN
и EMN
опираются на одну и ту же дугу, DE\parallel BC
(как средняя линия), а \angle ABC=\angle DMN
(как углы с соответственно перпендикулярными сторонами). Поэтому
\angle EMN=\angle EDN=\angle EDA=\angle ABC=\angle DMN.
Следовательно,
\angle ABC=\frac{1}{2}\angle EMD=15^{\circ}.
Тогда
\angle ACB=180^{\circ}-60^{\circ}-15^{\circ}=105^{\circ}.
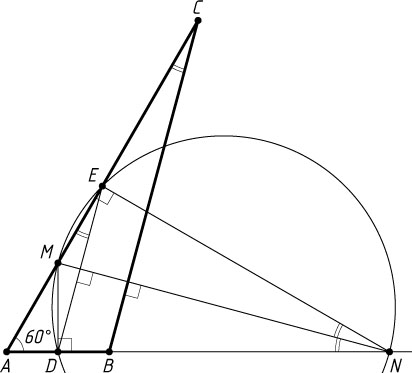
Если же \angle DME=150^{\circ}
(рис. 2), рассуждая аналогично, получим, что
\angle BAC=60^{\circ},~\angle ACB=15^{\circ},~\angle ABC=105^{\circ}.
Источник: Вступительный экзамен в МФТИ. — 1974, билет 6, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 74-6-4, с. 171
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 213, с. 26
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.37, с. 106

