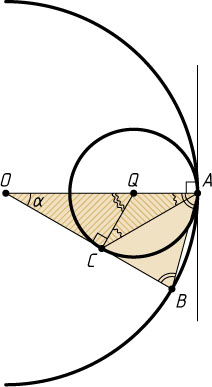
794. Две окружности касаются внутренним образом в точке A
. Из центра O
большей окружности проведён радиус OB
, касающийся меньшей окружности в точке C
. Найдите \angle BAC
.
Ответ. 45^{\circ}
.
Указание. Выразите искомый угол через угол AOB
.
Решение. Обозначим \angle AOB=\alpha
. Пусть Q
— центр меньшей окружности. Поскольку треугольник AOB
— равнобедренный, то
\angle OAB=\angle OBA=90^{\circ}-\frac{\alpha}{2}.
Поскольку треугольник OQC
— прямоугольный, то
\angle OQC=90^{\circ}-\alpha.
Но OQC
— внешний угол равнобедренного треугольника AQC
, поэтому
\angle QAC=\frac{1}{2}\angle OQC=45^{\circ}-\frac{\alpha}{2}.
Следовательно,
\angle BAC=\angle OAB-\angle QAC=45^{\circ}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 247, с. 30
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 247, с. 28
