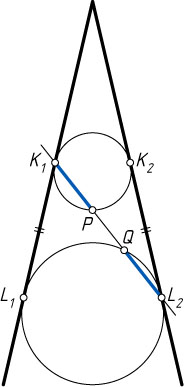
801. В угол вписаны две окружности; одна из них касается сторон угла в точках K_{1}
и K_{2}
, а другая — в точках L_{1}
и L_{2}
. Докажите, что прямая K_{1}L_{2}
высекает на этих двух окружностях равные хорды.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть P
и Q
— точки пересечения прямой K_{1}L_{2}
соответственно с первой и второй окружностью, отличные от точек K_{1}
и L_{2}
. По теореме о касательной и секущей
K_{1}Q\cdot K_{1}L_{2}=K_{1}L^{2}_{1},~L_{2}P\cdot K_{1}L_{2}=K_{2}L^{2}_{2}.
Поскольку K_{2}L_{2}=K_{1}L_{1}
, то K_{1}Q=L_{2}P
. Следовательно, K_{1}P=L_{2}Q
.
Источник: Московская математическая олимпиада. — 1970, XXXIII, 1-й тур, 10 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 17, с. 112
Источник: Журнал «Квант». — 1970, № 5, с. 41, М22(б)
Источник: Задачник «Кванта». — М22(б)
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.58(б), с. 66
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.64, с. 64
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.11, с. 24
