804. Обязательно ли треугольник равнобедренный, если центр вписанной в него окружности одинаково удалён от середин двух сторон?
Ответ. Нет.
Указание. Рассмотрите треугольник со сторонами 6, 8, 10.
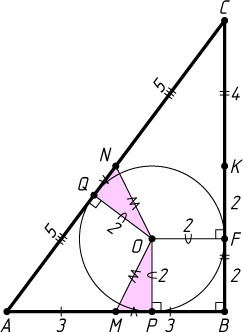
Решение. Рассмотрим прямоугольный треугольник ABC
с катетами AB=6
, BC=8
и гипотенузой AC=10
. Пусть O
— центр его вписанной окружности; M
, N
и K
— середины сторон AB
, AC
и BC
соответственно; P
, Q
и F
— точки касания вписанной окружности со сторонами соответственно AB
, AC
и BC
. Тогда
OP=OQ=OF=\frac{AB+BC-AC}{2}=\frac{6+8-10}{2}=2,
PM=BM-BP=\frac{1}{2}AB-OF=3-2=1,
QN=AN-AQ=\frac{1}{2}AC-AP=5-4=1.
Следовательно, OM=ON=\sqrt{5}
.
Источник: Всероссийская олимпиада школьников. — 1974-75, I, III этап, 9 класс
Источник: Яковлев Г. Н. и др. Всероссийские математические олимпиады школьников. — М.: Просвещение, 1992. — № 6, с. 7
