809. Дан треугольник ABC
. Прямая l
касается вписанной в него окружности. Обозначим через l_{a}
, l_{b}
, l_{c}
прямые, симметричные l
относительно биссектрис внешних углов треугольника. Докажите, что треугольник, образованный этими прямыми, равен треугольнику ABC
.
Решение. Лемма 1. Пусть l
— произвольная прямая, l_{a}
, l_{b}
и l_{c}
— прямые, симметричные l
относительно биссектрис внешних углов при вершинах соответственно A
, B
и C
треугольника ABC
. Тогда треугольник, образованный прямыми l_{a}
, l_{b}
и l_{c}
, подобен треугольнику ABC
.
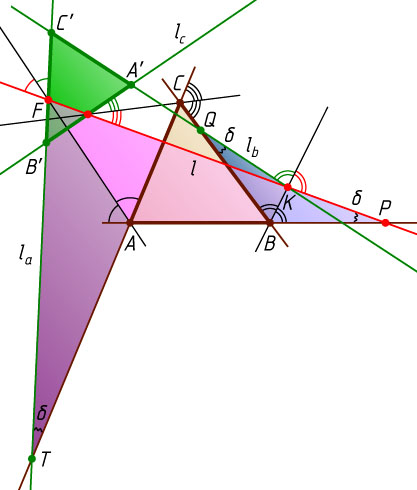
Действительно, пусть прямая l
пересекает биссектрису внешнего угла при вершине B
треугольника ABC
в точке K
(рис. 1), биссектрису внешнего угла при вершине A
— в точке F
, прямую AB
— в точке P
, прямые l_{b}
и BC
пересекаются в точке Q
, а прямые l_{a}
и AC
— в точке T
. Тогда треугольники BKP
и BKQ
симметричны относительно прямой BK
, поэтому \angle BPK=\angle BQK=\delta
. Аналогично \angle ATF=\angle APF=\angle BPK=\delta
. Следовательно, при повороте на угол \delta
по часовой стрелке прямая l_{b}
перейдёт в прямую, параллельную BC
, а прямая l_{a}
перейдёт в прямую, параллельную AC
. Значит, угол между прямыми l_{a}
и l_{b}
равен углу C
треугольника ABC
.
Аналогично докажем, что остальные углы треугольника, образованного прямыми l_{a}
, l_{b}
и l_{c}
, равны углам A
и B
треугольника ABC
. Отсюда следует доказательство леммы.
Лемма 2. Три прямые, симметричные относительно сторон треугольника прямой, проходящей через точку пересечения высот треугольника, пересекаются в одной точке.
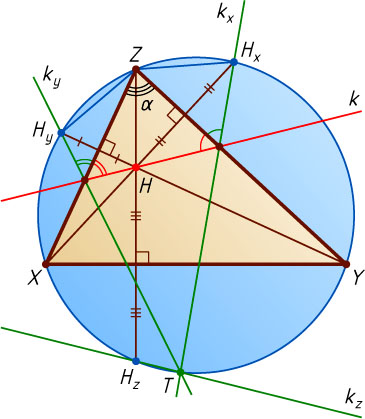
Действительно, пусть XYZ
— произвольный треугольник (рис. 2), H
— точка пересечения его высот, k
— прямая, проходящая через точку H
, k_{x}
и H_{x}
— образы прямой k
и точки H
при симметрии относительно прямой YZ
, k_{y}
и H_{y}
— относительно AC
, k_{z}
и H_{z}
— относительно AB
. Известно, что точки, симметричные H
относительно прямых ZY
, XZ
и YZ
, лежат на описанной окружности треугольника XYZ
.
Пусть прямые k_{y}
и k_{x}
пересекаются в точке T
. Обозначим \alpha
угол между прямыми ZX
и ZY
. Прямая k_{x}
получена из прямой k_{y}
композицией симметрий относительно прямых ZX
и ZY
, следовательно, прямая k_{y}
переходит в прямую k_{x}
при повороте на угол 180^{\circ}-2\alpha
, т. е.
\angle H_{y}TH_{x}=180^{\circ}-2\alpha=180^{\circ}-\angle H_{y}ZH_{x},
значит, точка T
пересечения прямых k_{y}
и k_{x}
лежит на описанной окружности треугольника XYZ
, т. е. прямые k_{x}
и k_{y}
пересекаются на этой окружности.
Аналогично докажем, что прямые k_{z}
и k_{x}
также пересекаются на этой окружности.
Прямые k_{z}
, k_{x}
и k_{y}
пересекают окружность в точках H_{z}
, H_{x}
и H_{y}
соответственно. Если треугольник не прямоугольный, то точки H_{z}
, H_{x}
и H_{y}
различны. Следовательно, вторые точки пересечения этих прямых с окружностью совпадают. Поэтому все три прямые пересекаются на описанной окружности треугольника XYZ
.
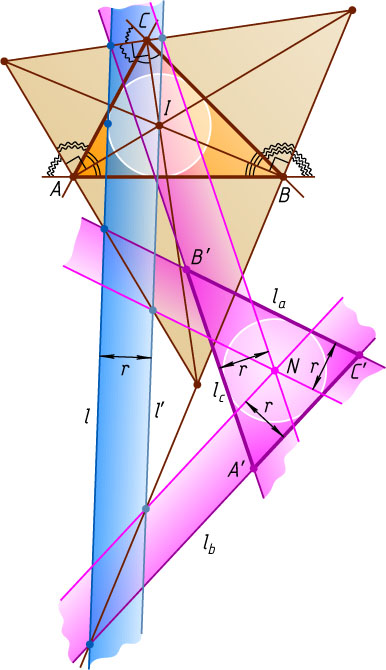
Перейдём к нашей задаче. Заметим, что центр I
вписанной окружности треугольника ABC
есть точка пересечения высот треугольника, образованного биссектрисами внешних углов треугольника ABC
(рис. 3). Пусть l
— произвольная прямая, касающаяся вписанной окружности треугольника ABC
, l'
— параллельная ей прямая, проходящая через точку I
. Тогда по лемме 2 прямые, симметричные l'
относительно сторон треугольника, образованного биссектрисами внешних углов треугольника ABC
, пересекаются в одной точке, а так как прямые l_{a}
, l_{b}
и l_{c}
удалены от этой точки N
на одно и то же расстояние, равное радиусу r
вписанной окружности треугольника ABC
, то точка N
равноудалена от сторон треугольника, образованного прямыми l_{a}
, l_{b}
, l_{c}
и подобного по лемме 1 треугольнику ABC
. Заметим, что точка N
— центр вписанной (а не вневписанной) окружности треугольника, образованного прямыми l_{a}
, l_{b}
, l_{c}
. Этот треугольник подобен треугольнику ABC
, причём коэффициент подобия равен отношению радиусов вписанных окружностей, т. е. 1. Следовательно, этот треугольник равен треугольнику ABC
. Что и требовалось доказать.
Автор: Заславский А. А.
Источник: Турнир городов. — 2011-2012, XXXIII, весенний тур, старшие классы, основной вариант
Источник: Московская математическая олимпиада. — 2012, LXXV, 9 класс
Источник: Журнал «Квант». — 2012, № 4, с. 50


