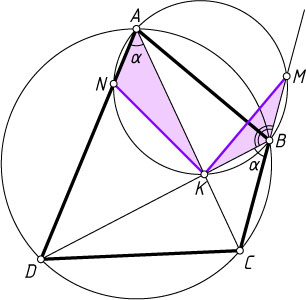
813. Четырёхугольник ABCD
вписан в окружность. Его диагонали пересекаются в точке K
. Окружность, проходящая через точки A
, B
и K
, пересекает прямые BC
и AD
в точках M
и N
. Докажите, что KM=KN
.
Решение. Пусть окружность радиуса R
, проходящая через точки A
, B
и K
, пересекает сторону AD
четырёхугольника ABCD
в точке N
, а продолжение стороны BC
— в точке M
. Обозначим \angle CAD=\alpha
. Вписанные углы CAD
и CBD
опираются на одну и ту же дугу, поэтому \angle CBD=\angle CAD=\alpha
. Тогда \angle MBK=180^{\circ}-\angle CBD=180^{\circ}-\alpha
.
По теореме синусов из треугольников AKN
и BKM
находим, что
KN=2R\sin\angle KAN=2R\sin\alpha,~KM=2R\sin\angle MBK=2R\sin(180^{\circ}-\alpha)=2R\sin\alpha.
Следовательно, KN=KM
.
Аналогично для остальных случаев.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 788, с. 98
