814. Высота прямоугольного треугольника ABC
, опущенная на гипотенузу AB
, равна h
; D
— основание высоты, M
и N
— середины отрезков AD
и DB
. Найдите расстояние от вершины C
до точки пересечения высот треугольника CMN
.
Ответ. \frac{3}{4}h
.
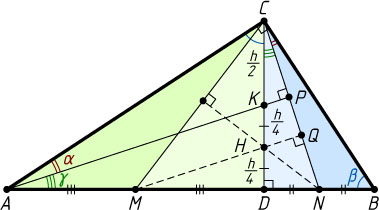
Решение. Первый способ. Пусть M
, N
и K
— середины отрезков AD
, DB
и CD
соответственно (рис. 1). Обозначим \angle ACD=\angle CBD=\beta
, \angle CAK=\alpha
, \angle DAK=\gamma
.
Треугольники ACD
и CBD
подобны по двум углам. При этом подобии медиана AK
треугольника ACD
соответствует медиане CN
треугольника ACD
, поэтому \angle BCN=\angle CAK=\alpha
и \angle DCN=\angle DAK=\gamma
.
Пусть P
— точка пересечения прямых AK
и CN
. Из треугольника ACP
находим, что
\angle APC=180^{\circ}-\alpha-\beta-\gamma=180^{\circ}-90^{\circ}=90^{\circ}.
Пусть прямая, проходящая через точку M
параллельно AP
, пересекает CD
и CN
в точках H
и Q
соответственно. Тогда MQ
— высота треугольника CMN
, MH
— средняя линия треугольника ADK
. Значит, H
— точка пересечения высот треугольника CMN
и H
— середина DK
. Следовательно,
CH=CK+KH=\frac{1}{2}h+\frac{1}{4}h=\frac{3}{4}h.
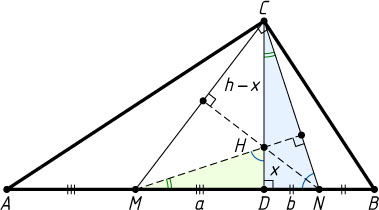
Второй способ. Пусть M
и N
— середины отрезков AD
и DB
соответственно (рис. 2), H
— точка пересечения высот треугольника CMN
. Обозначим DM=a
, DN=b
, DH=x
.
Поскольку CD=h
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла,
h^{2}=AD^{2}=AD\cdot BD=2a\cdot2b=4ab.
Прямоугольные треугольники MDH
и CDN
подобны по двум углам, поэтому \frac{DH}{DN}=\frac{DM}{CD}
, или \frac{x}{b}=\frac{a}{h}
, откуда
x=\frac{ab}{h}=\frac{\frac{h^{2}}{4}}{h}=\frac{h}{4}.
Следовательно,
CH=CD-DH=h-\frac{h}{4}=\frac{3}{4}h.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 181, с. 21

