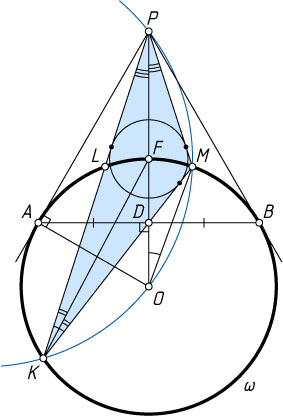
815. На окружности \omega
с центром O
взяты точки A
и B
. Касательные, проходящие через точки A
и B
, пересекаются в точке P
. Хорда MK
окружности \omega
проходит через середину AB
. Докажите, что пересечение отрезка OP
с окружностью \omega
есть центр вписанной в треугольник MKP
окружности.
Решение. Предположим, что точка M
расположена на меньшей дуге AB
окружности \omega
. Пусть эта окружность пересекает отрезки OP
и PK
в точках F
и L
соответственно, D
— середина хорды AB
.
Поскольку AD
— высота прямоугольного треугольника OAP
, проведённая из вершины прямого угла, DP\cdot DO=AD^{2}
. С другой стороны, по теореме о произведении отрезков пересекающихся хорд DK\cdot DM=AD\cdot DB=AD^{2}
. Из равенства DP\cdot DO=DK\cdot DM
следует, что точки O
, K
, P
и M
лежат на одной окружности (см. задачу 114). Вписанные в эту окружность углы PKM
и POM
опираются на одну и ту же дугу, поэтому \angle FOM=\angle POM=\angle PKM=\angle LKM
.
Угол FOM
— центральный угол окружности \omega
, а LKM
— вписанный, поэтому F
— середина меньшей дуги LM
. Значит, \angle FKM=\angle FKL=\angle FKP
, т. е. KF
— биссектриса угла MKP
треугольника MKP
. Аналогично MF
— также биссектриса этого треугольника. Следовательно, F
— точка пересечения биссектрис треугольника MKP
, т. е. центр вписанной окружности этого треугольника.
Автор: Маркелов С. В.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1022, с. 125
