820. Через точку M
, расположенную вне данной окружности, проведены две секущие. Одна из них проходит через центр O
окружности и пересекает её в точках A
и B
. Вторая секущая пересекает окружность в точках C
и D
. Окружности, описанные около треугольников AOC
и BOD
, вторично пересекаются в точке P
. Докажите, что \angle MPO=90^{\circ}
.
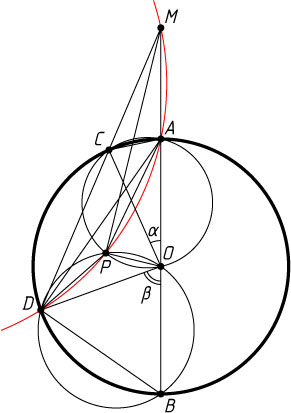
Решение. Предположим, что точка C
лежит между M
и D
, а точка A
— между M
и O
. Докажем, что точки M
, A
, P
и D
лежат на одной окружности.
Обозначим \angle AOC=\alpha
, \angle BOD=\beta
. Тогда \angle BMD=\frac{1}{2}(\beta-\alpha)
как угол между секущими к окружности с диаметром AB
. Из равнобедренного треугольника BOD
находим, что \angle OBD=90^{\circ}-\frac{\beta}{2}
, а так как четырёхугольник OBDP
вписанный, то
\angle OPD=180^{\circ}-\angle OBD=90^{\circ}+\frac{\beta}{2}.
Из равнобедренного треугольника OAC
находим, что \angle ACO=90^{\circ}-\frac{\alpha}{2}
. Вписанные в окружность углы APO
и ACO
опираются на одну и ту же дугу, поэтому \angle APO=\angle ACO=90^{\circ}-\frac{\alpha}{2}
. Значит,
\angle APD=360^{\circ}-\angle OPD-\angle APO=360^{\circ}-\left(90^{\circ}+\frac{\beta}{2}\right)-\left(90^{\circ}-\frac{\alpha}{2}\right)=180^{\circ}-\frac{\beta}{2}+\frac{\alpha}{2}.
Следовательно,
\angle APD+\angle AMD=\frac{1}{2}(\beta-\alpha)+180^{\circ}-\frac{\beta}{2}+\frac{\alpha}{2}=180^{\circ}.
Поэтому MAPD
— вписанный четырёхугольник, т. е. точки M
, A
, P
и D
лежат на одной окружности.
Вписанные в эту окружность углы APM
и ADM
опираются на одну и ту же дугу, поэтому
\angle APM=\angle ADM=\angle ADC=\frac{1}{2}\angle AOC=\frac{\alpha}{2},
Следовательно,
\angle MPO=\angle MPA+\angle APO=\angle MPA+\angle ACO=\frac{\alpha}{2}+\left(90^{\circ}-\frac{\alpha}{2}\right)=90^{\circ}.
Что и требовалось доказать.
Аналогично для любого другого расположения точек A
, B
, C
и D
на данных секущих.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 840, с. 103
