821. Найдите углы треугольника, ортотреугольник которого (треугольник с вершинами в основаниях высот данного) подобен исходному треугольнику.
Ответ. \frac{\pi}{3}
, \frac{\pi}{3}
и \frac{\pi}{3}
или \frac{\pi}{7}
, \frac{2\pi}{7}
и \frac{4\pi}{7}
.
Решение. Пусть AA_{1}
, BB_{1}
и CC_{1}
— высоты треугольника ABC
, \alpha
, \beta
и \gamma
— углы треугольника ABC
, противолежащие сторонам BC
, AC
и AB
соответственно.
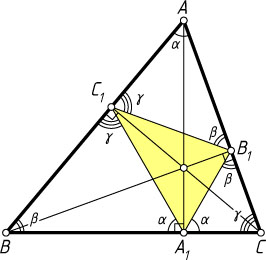
1) Предположим, что треугольник ABC
остроугольный (рис. 1). Тогда
\angle B_{1}A_{1}C_{1}=\pi-\angle BA_{1}C_{1}-\angle CA_{1}B_{1}=\pi-\angle BAC-\angle BAC=\pi-2\alpha
(см. задачу 141). Аналогично \angle A_{1}B_{1}C_{1}=\pi-2\beta
и \angle A_{1}C_{1}B_{1}=\pi-2\gamma
.
Если \pi-2\alpha=\alpha
, \pi-2\beta=\beta
и \pi-2\gamma=\gamma
, то \alpha=\beta=\gamma=\frac{\pi}{3}
, т. е. треугольник ABC
— равносторонний.
Если \pi-2\alpha=\alpha
, \pi-2\beta=\gamma
и \pi-2\gamma=\beta
, то \alpha=\frac{\pi}{3}
и \gamma=\beta
. В этом случае треугольник ABC
— также равносторонний.
Если \pi-2\alpha=\beta
, \pi-2\beta=\gamma
и \pi-2\gamma=\alpha
, то \alpha=\beta=\gamma=\frac{\pi}{3}
, т. е. и в этом случае треугольник ABC
— равносторонний.
Аналогично для любого другого случая.
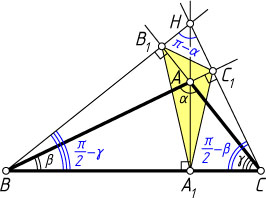
2) Предположим, что треугольник ABC
тупоугольный, причём \alpha\gt\frac{\pi}{2}
(рис. 2). Пусть его высоты пересекаются в точке H
. Тогда A_{1}B_{1}C_{1}
— ортотреугольник остроугольного треугольника HBC
с углами
\angle CBH=\frac{\pi}{2}-\angle BCB_{1}=\frac{\pi}{2}-\gamma,
\angle BCH=\frac{\pi}{2}-\angle CBC_{1}=\frac{\pi}{2}-\beta,
\angle BHC=\pi-\angle B_{1}AC_{1}=\pi-\alpha.
Значит,
\angle B_{1}A_{1}C_{1}=\pi-2\angle BHC=\pi-2(\pi-\alpha)=2\alpha-\pi,
\angle A_{1}B_{1}C_{1}=\pi-2\angle BCH=\pi-2\left(\frac{\pi}{2}-\beta\right)=2\beta,
\angle A_{1}C_{1}B_{1}=\pi-2\angle CBH=\pi-2\left(\frac{\pi}{2}-\gamma\right)=2\gamma.
Ясно, что 2\alpha-\pi\ne\alpha
. Случай \alpha-\pi=\beta
, 2\gamma=\alpha
, 2\beta=\beta
также невозможен.
Если 2\gamma=\alpha
, 2\beta=\gamma
и 2\alpha-\pi=\beta
, то \beta=\frac{\pi}{7}
, \gamma=\frac{2\pi}{7}
, \alpha=\frac{4\pi}{7}
.
Аналогично для случая 2\beta=\alpha
, 2\gamma=\beta
и 2\alpha-\pi=\gamma
.
Следовательно, условию задачи удовлетворяют два вида треугольников: равносторонние и треугольники с углами \frac{\pi}{7}
, \frac{2\pi}{7}
и \frac{4\pi}{7}
.
Примечание. См. также статью А.Егорова «Ортоцентрический треугольник», Квант, 2001, N4, с.36-38.
Автор: Куценок В. Е.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 806, с. 100
Источник: Международная олимпиада «Интеллектуальный марафон». — 1995, V, задачи индивидуальных соревнований, задача 2