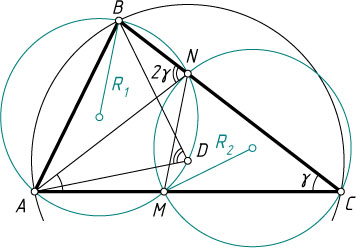
833. Точка D
— центр окружности, описанной около остроугольного треугольника ABC
. Окружность, проходящая через точки A
, B
и D
, пересекает стороны AC
и BC
в точках M
и N
соответственно. Докажите, что окружности, описанные около треугольников ABD
и MNC
, равны.
Указание. Докажите, что \angle NAC=\angle ACB
.
Решение. Обозначим \angle ACB=\gamma
. Тогда
\angle ANB=\angle ADB=2\gamma
как углы, вписанные в окружность, проходящую через точки A
, B
и D
. Поэтому
\angle NAC=\angle ANB-\angle ACN=2\gamma-\gamma=\gamma.
Пусть R_{1}
и R_{2}
— радиусы окружностей, описанных около треугольников ABD
и MNC
соответственно. Тогда
MN=2R_{1}\sin\angle NAC=2R_{1}\sin\gamma,~MN=2R_{2}\sin\angle NCM=2R_{2}\sin\gamma.
Следовательно, R_{1}=R_{2}
.
Автор: Чиник Б. И.
Источник: Журнал «Математика в школе». — № 6, 1991, с. 38
Источник: Всесоюзная олимпиада по математике. — 1991, XXV
