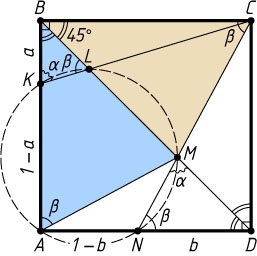
834. На сторонах AB
и AD
квадрата ABCD
взяты точки K
и N
соответственно. При этом AK\cdot AN=2BK\cdot DN
. Отрезки CK
и CN
пересекают диагональ BD
в точках L
и M
. Докажите, что точки K
, L
, M
, N
и A
лежат на одной окружности.
Указание. Докажите, что \angle BKC+\angle DNC=135^{\circ}
.
Решение. Пусть сторона квадрата равна 1. Обозначим
BK=a,~DN=b,~\angle BKC=\alpha,~\angle DNC=\beta.
Тогда
a=\cos\alpha,~b=\cos\beta,~(1-a)(1-b)=2ab.
Отсюда следует, что 1-ab=a+b
.
Поскольку
\tg\alpha=\frac{1}{a},~\tg\beta=\frac{1}{b},
то
\tg(\alpha+\beta)=\frac{\frac{1}{a}+\frac{1}{b}}{1-\frac{1}{ab}}=\frac{a+b}{ab-1}=-1.
Поэтому \alpha+\beta=135^{\circ}
. Тогда
\angle BLK=135^{\circ}-\alpha=\beta=\angle CND=\angle BCM=\angle BAM
(из равенства треугольников BCM
и BAM
по двум сторонам и углу между ними). Следовательно,
\angle KLM+\angle KAM=180^{\circ}.
Поэтому точки K
, L
, M
и A
принадлежат одной окружности. Аналогично докажем, что точки A
, N
, M
и L
лежат на одной (той же) окружности.
Автор: Терёшин Д. А.
Источник: Журнал «Математика в школе». — № 6, 1991, с. 38
Источник: Всесоюзная олимпиада по математике. — 1991
