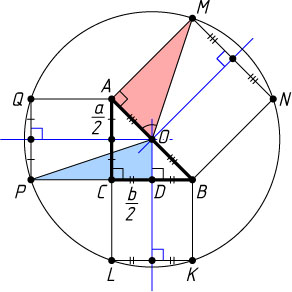
836. На сторонах прямоугольного треугольника, вне его, построены квадраты. Известно, что шесть вершин квадратов, не принадлежащих треугольнику, лежат на окружности радиуса 1. Найдите стороны треугольника.
Ответ. \frac{\sqrt{2}}{\sqrt{5}}
, \frac{\sqrt{2}}{\sqrt{5}}
, \frac{2}{\sqrt{5}}
.
Указание. Центр данной окружности — середина гипотенузы данного треугольника.
Решение. Пусть вершины M
, N
, K
, L
, P
, Q
квадратов AMNB
, CBKL
и ACPQ
, построенных на гипотенузе AB
и катетах BC
и AC
, лежат на окружности радиуса 1. Центр этой окружности есть точка пересечения серединных перпендикуляров к отрезкам MN
, KL
и PQ
. Эти перпендикуляры являются также серединными перпендикулярами к сторонам треугольника ABC
. Следовательно, их точка пересечения совпадает с серединой O
гипотенузы AB
.
Из прямоугольного треугольника AOM
находим, что \tg\angle MOA=2
. Поэтому
AO=OM\cos\angle MOA=\frac{1}{\sqrt{5}},~AB=\frac{2}{\sqrt{5}}.
Пусть D
— проекция точки O
на BC
. Обозначим BC=a
, AC=b
. Тогда a^{2}+b^{2}=\frac{4}{5}
. По теореме Пифагора
OD^{2}+DP^{2}=OP^{2},~\mbox{или}~\left(\frac{b}{2}\right)^{2}+\left(b+\frac{a}{2}\right)^{2}=1.
Из полученной системы уравнений находим, что a=b=\frac{\sqrt{2}}{\sqrt{5}}
.
Источник: Вступительное задание ЗФТШ при МФТИ. —
