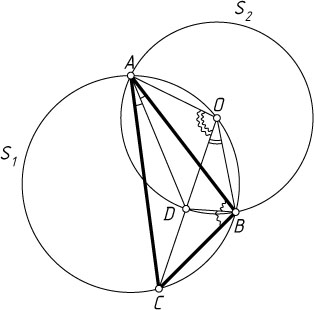
837. Окружности S_{1}
и S_{2}
пересекаются в точках A
и B
, причём центр O
окружности S_{2}
лежит на окружности S_{1}
. Хорда OC
окружности S_{1}
пересекает окружность S_{2}
в точке D
. Докажите, что D
— точка пересечения биссектрис треугольника ABC
.
Указание. Используя свойства вписанных углов, докажите, что \angle BAD=\frac{1}{2}\angle BAC
.
Решение. Докажем, что AD
— биссектриса угла BAC
. Действительно, \angle BOC=\angle BAC
(углы, вписанные в окружность S_{1}
, опирающиеся на одну и ту же дугу), а
\angle BAD=\frac{1}{2}\angle BOD=\frac{1}{2}\angle BAC.
Аналогично докажем, что BD
— биссектриса угла ABC
.
Источник: Журнал «Квант». — 1990, № 10, с. 70
Источник: Всероссийская олимпиада школьников. — 1990, XVI, 10 класс
