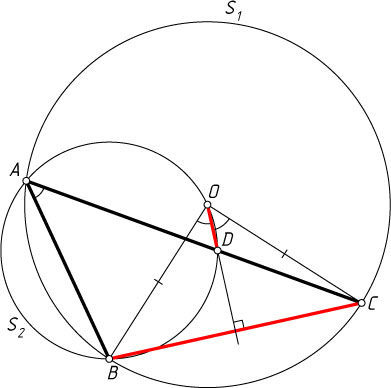
838. Окружности S_{1}
и S_{2}
пересекаются в точках A
и B
, причём центр O
окружности S_{1}
лежит на окружности S_{2}
. Хорда AC
окружности S_{1}
пересекает окружность S_{2}
в точке D
. Докажите, что отрезки OD
и BC
перпендикулярны.
Указание. Докажите, что OD
— биссектриса угла BOC
.
Решение. Поскольку
\angle BOD=\angle BAD=\angle BAC=\frac{1}{2}\angle BOC,
то OD
— биссектриса угла BOC
при вершине равнобедренного треугольника BOC
. Следовательно, OD\perp BC
.
Примечание. См. также статью В.Уроева и М.Шабунина «Об углах и окружностях», Квант, 1991, N1, с.54-58.
Источник: Всероссийская олимпиада школьников. — 1990
Источник: Журнал «Квант». — 1990, № 10, с. 69
Источник: Журнал «Математика в школе». — 1991, № 1, с. 58, задача 7
