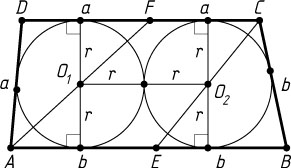
841. В выпуклом четырёхугольнике ABCD
заключены две окружности одинакового радиуса r
, касающиеся друг друга внешним образом. Центр первой окружности находится на отрезке, соединяющем вершину A
с серединой F
стороны CD
, а центр второй окружности находится на отрезке, соединяющем вершину C
с серединой E
стороны AB
. Первая окружность касается сторон AB
, AD
и CD
, а вторая окружность касается сторон AB
, BC
и CD
. Найдите AC
.
Ответ. 2r\sqrt{5}
.
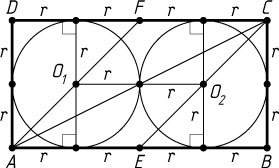
Указание. Докажите, что ABCD
— прямоугольник.
Решение. Обозначим AD=a
, BC=b
. Поскольку AF
и CE
— биссектрисы углов A
и C
, то треугольники ADF
и CBE
— равнобедренные. Поэтому
CD=2DF=2AD=2a,~AB=2BE=2BC=2b.
Пусть O_{1}
и O_{2}
— центры соответственно первой и второй окружностей. Тогда O_{1}O_{2}
— средняя линия трапеции (или параллелограмма) AFCE
, поэтому
2r=O_{1}O_{2}=\frac{1}{2}(CF+AE)=\frac{a+b}{2}.
С другой стороны, 2r\leqslant a
и 2r\leqslant b
. Если хотя бы одно из этих неравенств строгое, то
2r\lt\frac{a+b}{2}.
Значит, a=2r
и b=2r
. Тогда ABCD
— прямоугольник со сторонами 2r
, 2r
, 4r
, 4r
, поэтому
AC^{2}=BC^{2}+AB^{2}=4r^{2}+16r^{2}=20r^{2}.
Следовательно, AC=2r\sqrt{5}
.
