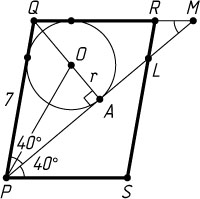
844. В параллелограмме PQRS
биссектриса угла при вершине P
, равного 80^{\circ}
, пересекает сторону RS
в точке L
. Найдите радиус окружности, касающейся отрезка PQ
и лучей QR
и PL
, если известно, что PQ=7
.
Ответ. 7\cos40^{\circ}\tg20^{\circ}
.
Указание. Пусть M
— точка пересечения прямых PL
и QR
. Искомая окружность вписана в равнобедренный треугольник PQM
.
Решение. Пусть M
— точка пересечения прямых PL
и QR
, O
— центр указанной окружности, r
— её радиус, A
— точка касания окружности с лучом PL
. Тогда
\angle QMP=\angle SPM=\angle QPM=40^{\circ}.
Поэтому треугольник PQM
— равнобедренный,
PA=PQ\cos40^{\circ}=7\cos40^{\circ},~r=OA=AP\tg20^{\circ}=7\cos40^{\circ}\tg20^{\circ}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1988, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 15
