849. Окружность радиуса 2 касается окружности радиуса 4 в точке B
. Прямая, проходящая через точку B
, пересекает окружность меньшего радиуса в точке A
, а большего радиуса — в точке C
. Найдите BC
, если AC=3\sqrt{2}
.
Ответ. 2\sqrt{2}
.
Решение. Пусть O_{1}
и O_{2}
— центры меньшей и большей окружностей соответственно. Поскольку \angle ABO_{1}=\angle CBO_{2}
, и треугольники ABO_{1}
и CBO_{2}
равнобедренные, то эти треугольники подобны и коэффициент подобия равен отношению радиусов окружностей, т. е. \frac{1}{2}
.
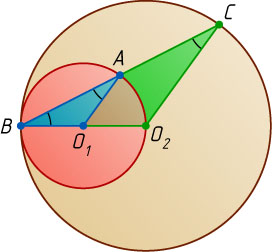
Если окружности касаются внутренним образом, то
BC=2AC=6\sqrt{2},
что невозможно, так как хорда BC
большей окружности не может быть больше диаметра этой окружности, равного 8.
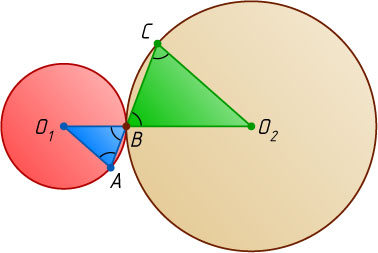
Если окружности касаются внешним образом, то
BC=\frac{2}{3}AC=\frac{2}{3}\cdot3\sqrt{2}=2\sqrt{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1986, вариант 2, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 10
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.42, с. 71

