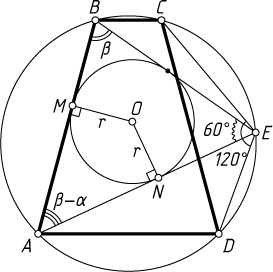
850. Трапеция ABCD
с основаниями BC
и AD
вписана в окружность. На дуге CD
взята точка E
и соединена со всеми вершинами трапеции. Известно, что \angle CED=120^{\circ}
, \angle ABE-\angle BAE=\alpha
. Найдите отношение периметра треугольника ABE
к радиусу вписанной в него окружности.
Ответ. 2\left(\ctg\left(30^{\circ}-\frac{\alpha}{4}\right)+\ctg\left(30^{\circ}+\frac{\alpha}{4}\right)+\sqrt{3}\right)
.
Указание. \angle AEB=60^{\circ}
.
Решение. Поскольку BC\parallel AD
, то
\cup AB=\cup CD=360^{\circ}-\cup CAD=360^{\circ}-2\angle CED=
=360^{\circ}-240^{\circ}=120^{\circ}.
Поэтому \angle AEB=60^{\circ}
.
Обозначим \angle ABE=\beta
. Тогда
\angle BAE=\beta-\alpha,~\beta-\alpha+\beta+60^{\circ}=180^{\circ}.
Отсюда находим, что
\angle ABE=\beta=60^{\circ}+\frac{\alpha}{2},~\angle BAE=\beta-\alpha=60^{\circ}-\frac{\alpha}{2}.
Пусть O
— центр окружности, вписанной в треугольник ABE
, r
— её радиус, M
и N
— точки касания этой окружности со сторонами AB
и AE
соответственно, P
— периметр треугольника ABE
. Тогда
P=2(BM+AM+EN)=
=2\left(r\ctg\left(30^{\circ}+\frac{\alpha}{4}\right)+r\ctg\left(30^{\circ}-\frac{\alpha}{4}\right)+r\sqrt{3}\right)=
=2r\left(\ctg\left(30^{\circ}+\frac{\alpha}{4}\right)+\ctg\left(30^{\circ}-\frac{\alpha}{4}\right)+\sqrt{3}\right).
Следовательно,
\frac{P}{r}=2\left(\ctg\left(30^{\circ}-\frac{\alpha}{4}\right)+\ctg\left(30^{\circ}+\frac{\alpha}{4}\right)+\sqrt{3}\right).
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1981, № 4, вариант 1
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 11
