851. Пятиугольник ABCDE
вписан в окружность. Известно, что BD\parallel AE
и \angle CAE=2\angle CEA
, \angle CBD-\angle CDB=\alpha
. Найдите отношение периметра треугольника ACE
к радиусу описанной около него окружности.
Ответ. 2(\sin\alpha+\sin2\alpha+\sin3\alpha)
.
Указание. \angle CEA=\alpha
.
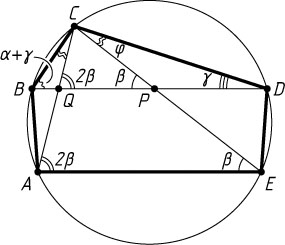
Решение. Обозначим
\angle AEC=\beta,~\angle CDB=\gamma,~\angle ECD=\varphi.
Тогда \angle CAE=2\beta
.
Пусть P
и Q
— точки пересечения отрезка BD
с отрезками CE
и AC
соответственно. Поскольку AE\parallel BD
, то
\cup AB=\cup ED,~\angle ACB=\angle ECD=\varphi,
\angle QPC=\angle AEC=\beta,~\angle PQC=\angle CAE=2\beta.
По теореме о внешнем угле треугольника
\angle QPC=\angle PDC+\angle PCD,~\mbox{или}~\beta=\gamma+\varphi,
\angle PQC=\angle QBC+\angle QCB,~\mbox{или}~2\beta=\alpha+\gamma+\varphi.
Отсюда следует, что \beta=\alpha
.
Если R
— радиус данной окружности, то
AC+CE+AE=
=2R\sin\angle CEA+2R\sin\angle CAE+2R\sin\angle ACE=
=2R\sin\beta+2R\sin2\beta+2R\sin(180^{\circ}-3\beta)=
=2R\sin\alpha+2R\sin2\alpha+2R\sin3\alpha.
Следовательно,
\frac{AC+CE+AE}{R}=2(\sin\alpha+\sin2\alpha+\sin3\alpha).
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1981, № 4, вариант 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 11
