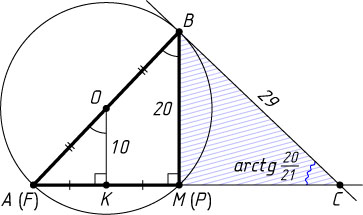
856. Около нетупоугольного треугольника AMB
описана окружность, центр которой удалён от стороны AM
на расстояние 10. Продолжение стороны AM
за вершину M
отсекает от касательной к окружности, проведённой через вершину B
, отрезок CB
, равный 29. Найдите площадь треугольника CMB
, если известно, что угол ACB
равен \arctg\frac{20}{21}
.
Ответ. 210.
Указание. Докажите, что треугольник AMB
— прямоугольный.
Решение. Пусть O
— центр данной окружности, K
— середина стороны AM
, P
— проекция точки B
на прямую AC
, F
— точка пересечения луча BO
с прямой AC
. Тогда
BP=CB\sin\angle C=29\cdot\frac{20}{29}=20.
Точка O
находится между точками B
и F
, так как \angle ABM\leqslant90^{\circ}
. Поскольку OK=10
, точка O
— середина BF
, т. е. точка F
лежит на окружности. Значит, точки A
и F
совпадают и AB
— диаметр окружности. Следовательно, точки P
и M
также совпадают и
S_{\triangle CMB}=\frac{1}{2}CM\cdot MB=10\sqrt{29^{2}-20^{2}}=210.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1978, вариант 3, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 23
