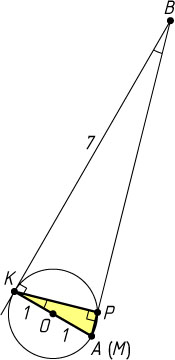
857. Около треугольника APK
описана окружность радиуса 1. Продолжение стороны AP
за вершину P
отсекает от касательной к окружности, проведённой через вершину K
, отрезок BK
, равный 7. Найдите площадь треугольника APK
, если известно, что угол ABK
равен \arctg\frac{2}{7}
.
Ответ. \frac{28}{53}
.
Указание. Докажите, что треугольник APK
— прямоугольный.
Решение. Пусть O
— центр данной окружности. Продолжим KO
до вторичного пересечения с окружностью в точке M
. Из прямоугольного треугольника BKM
находим, что
\tg\angle MBK=\frac{KM}{BK}=\frac{2}{7}.
Следовательно, \angle MBK=\angle ABK
и треугольник APK
— прямоугольный. Поэтому
\angle AKP=\angle ABK,~AP=AK\sin\angle AKP=2\cdot\frac{2}{\sqrt{53}}=\frac{4}{\sqrt{53}},
PK=BK\sin\angle ABK=7\cdot\frac{2}{\sqrt{53}}=\frac{14}{\sqrt{53}}.
Следовательно,
S_{\triangle APK}=\frac{1}{2}AP\cdot PK=\frac{28}{53}.
