859. Длина окружности, описанной около равнобедренного треугольника, в три раза больше длины окружности, вписанной в этот треугольник. Найдите углы треугольника.
Ответ. \arccos\left(\frac{1}{2}\pm\frac{1}{2\sqrt{3}}\right)
; 180^{\circ}-2\arccos\left(\frac{1}{2}\pm\frac{1}{2\sqrt{3}}\right)
.
Указание. Выразите двумя способами основание треугольника: через радиус описанной окружности и угол при основании; через радиус вписанной окружности и угол при основании.
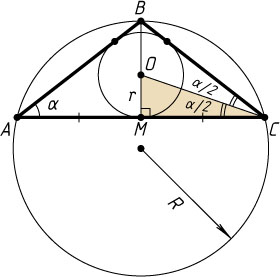
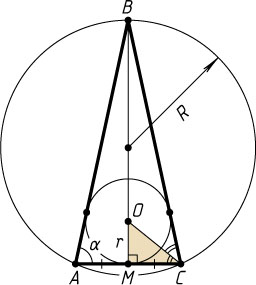
Решение. Пусть \alpha
— угол при основании AC
равнобедренного треугольника ABC
, r
и R
— радиусы вписанной и описанной окружностей (R=3r
), O
— центр вписанной окружности, M
— середина AC
. Тогда
AC=2R\sin\angle B=2R\sin(180^{\circ}-2\alpha)=2R\sin2\alpha.
В прямоугольном треугольнике OMC
\frac{1}{2}AC=MC=OM\ctg\frac{\alpha}{2}=r\ctg\frac{\alpha}{2}.
Поэтому AC=2r\ctg\frac{\alpha}{2}
. Приравняв найденные выражения для AC
, получим, что
R\sin2\alpha=r\ctg\frac{\alpha}{2}.
Поскольку R=3r
, то 3\sin2\alpha\tg\frac{\alpha}{2}=1
. Преобразуем левую часть этого уравнения:
6\sin\alpha\cos\alpha\tg\frac{\alpha}{2}=1,~12\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}\cos\alpha\tg\frac{\alpha}{2}=1,~12\sin^{2}\frac{\alpha}{2}\cos\alpha=1,
6(1-\cos\alpha)\cos\alpha=1,~6\cos^{2}\alpha-6\cos\alpha+1=0.
Следовательно, \cos\alpha=\frac{1}{2}\pm\frac{1}{2\sqrt{3}}
.
Источник: Вступительный экзамен на физический факультет МГУ. — 1977, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 28

