864. Около окружности радиуса R
описан параллелограмм. Площадь четырёхугольника с вершинами в точках касания окружности и параллелограмма равна S
. Найдите стороны параллелограмма.
Ответ. \frac{4R^{3}}{S}
.
Указание. Данный параллелограмм — ромб. Четырёхугольник с вершинами в точках касания — прямоугольник с острым углом между диагоналями, равным острому углу ромба.
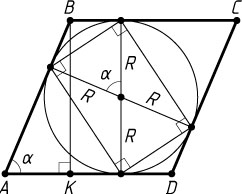
Решение. В данный параллелограмм ABCD
вписана окружность, поэтому ABCD
— ромб. Пусть A
— его острый угол. Четырёхугольник с вершинами в точках касания — прямоугольник с диагоналями, равными 2R
. Обозначим угол между ними через \alpha
. Тогда
S=\frac{1}{2}2R\cdot2R\sin\alpha=2R^{2}\sin\alpha,
откуда \sin\alpha=\frac{S}{2R^{2}}
.
Пусть K
— проекция точки B
на сторону AD
. Тогда
AB=\frac{BK}{\sin\angle A}=\frac{2R}{\sin\alpha}=\frac{2R}{\frac{S}{2R^{2}}}=\frac{4R^{3}}{S}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1979, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 53
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.32, с. 88
