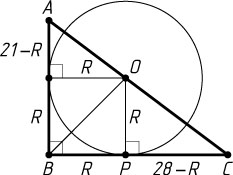
870. В прямоугольном треугольнике ABC
катет AB
равен 21, а катет BC
равен 28. Окружность, центр O
которой лежит на гипотенузе AC
, касается обоих катетов. Найдите радиус окружности.
Ответ. 12.
Указание. Пусть P
— точка касания окружности с катетом BC
. Рассмотрите подобные треугольники CPO
и CBA
.
Решение. Первый способ. Пусть P
— точка касания окружности с катетом BC
. Обозначим через R
радиус окружности. Из подобия треугольников CPO
и CBA
следует, что
\frac{28-R}{R}=\frac{28}{21}.
Отсюда находим, что R=12
.
Второй способ. Обозначим через R
радиус окружности. Тогда
S_{\triangle AOB}=\frac{1}{2}AB\cdot R=\frac{21R}{2},~S_{\triangle COB}=\frac{1}{2}BC\cdot R=14R.
Поскольку
S_{\triangle AOB}+S_{\triangle COB}=S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}\cdot21\cdot28,
имеем уравнение
\frac{21R}{2}+14R=\frac{1}{2}\cdot21\cdot28,
из которого находим, что R=12
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1981, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 54
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.6, с. 111
