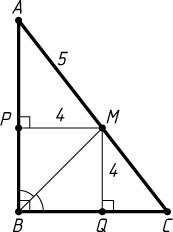
871. В прямоугольном треугольнике ABC
биссектриса прямого угла B
пересекает гипотенузу AC
в точке M
. Найдите площадь треугольника ABC
, если расстояние от точки M
до катета BC
равно 4, а AM=5
.
Ответ. \frac{98}{3}
.
Указание. Пусть P
и Q
— проекции точки M
на катеты AB
и BC
. Рассмотрите подобные треугольники MQC
и APM
Решение. Пусть P
и Q
— проекции точки M
на катеты AB
и BC
. По свойству биссектрисы PM=MQ=4
.
Из прямоугольного треугольника APM
находим, что
AP=\sqrt{AM^{2}-PM^{2}}=3.
Из подобия треугольников MQC
и APM
находим, что
QC=\frac{PM\cdot MQ}{AP}=\frac{4\cdot4}{3}=\frac{16}{3}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}(3+4)\left(4+\frac{16}{3}\right)=\frac{98}{3}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1981, вариант 3, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 72
