875. В равнобедренный треугольник ABC
(AB=BC)
вписана окружность радиуса 3. Прямая l
касается этой окружности и параллельна прямой AC
. Расстояние от точки B
до прямой l
равно 3. Найдите расстояние между точками, в которых данная окружность касается сторон AB
и BC
.
Ответ. 3\sqrt{3}
.
Указание. Рассмотрите прямоугольный треугольник OBQ
, где O
— центр окружности, P
— точка касания окружности со стороной BC
.
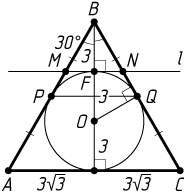
Решение. Пусть P
и Q
— точки касания окружности со сторонами AB
и BC
треугольника ABC
, O
— центр окружности, F
— точка касания окружности с прямой l
, M
и N
— точки пересечения прямой l
со сторонами AB
и BC
. Тогда треугольник MBN
подобен треугольнику ABC
. Поэтому он равнобедренный. Следовательно,
MF=MP=BP-BM=BQ-BN=NQ=NF.
Поэтому F
— середина MN
. Тогда луч BF
— биссектриса угла B
. Значит, точка F
лежит на отрезке BO
и
BO=BF+OF=3+3=6.
Из прямоугольного треугольника BQO
находим, что \angle OBQ=30^{\circ}
. Поэтому
\angle OQP=30^{\circ},~\frac{1}{2}PQ=OQ\cos\angle OQP=3\cos30^{\circ}=\frac{3\sqrt{3}}{2}.
Следовательно, PQ=3\sqrt{3}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1982, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 63
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.32, с. 76
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.32.1, с. 82
