876. Центр окружности радиуса 6, касающейся сторон AB
, BC
и CD
равнобедренной трапеции ABCD
, лежит на её большем основании AD
. Основание BC
равно 4. Найдите расстояние между точками, в которых окружность касается боковых сторон AB
и CD
этой трапеции.
Ответ. \frac{36}{5}
.
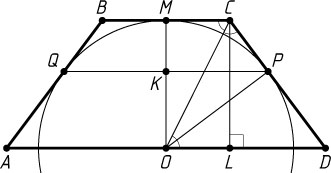
Указание. Пусть O
— центр окружности; Q
, M
и P
— точки её касания со сторонами соответственно AB
, BC
и CD
трапеции ABCD
; L
— проекция вершины C
на основание AD
; K
— точка пересечения отрезков PQ
и MO
. Найдите CD
из равнобедренного треугольника OCD
и рассмотрите подобные треугольники OKP
и DLC
.
Решение. Пусть O
— центр окружности; Q
, M
и P
— точки её касания со сторонами соответственно AB
, BC
и CD
трапеции ABCD
; L
— проекция вершины C
на основание AD
; K
— точка пересечения отрезков PQ
и MO
. Заметим, что PQ\parallel AD
(BQ=BM=CM=CP
).
Поскольку CO
— биссектриса угла BCD
, то \angle COD=\angle OCB=\angle OCD
, поэтому треугольник OCD
— равнобедренный, CD=OD
.
Обозначим CD=OD=x
. Тогда LD=OD-OL=OD-MC=x-2
. По теореме Пифагора из прямоугольного треугольника CLD
находим, что
CD^{2}=CL^{2}+LD^{2},~\mbox{или}~x^{2}=36+(x-2)^{2}.
Отсюда следует, что x=10
.
Из подобия треугольников OKP
и DLC
находим, что \frac{KP}{CL}=\frac{OP}{CD}
. Поэтому
KP=\frac{OP\cdot CL}{CD}=6\cdot\frac{6}{10}=\frac{18}{5}.
Следовательно, PQ=2KP=\frac{36}{5}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1982, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 64
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 2, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 165
