879. На плоскости даны две окружности радиусов 12 и 7 с центрами в точках O_{1}
и O_{2}
, касающиеся некоторой прямой в точках M_{1}
и M_{2}
и лежащие по одну сторону от этой прямой. Отношение длины отрезка M_{1}M_{2}
к длине отрезка O_{1}O_{2}
равно \frac{2\sqrt{5}}{5}
. Найдите M_{1}M_{2}
.
Ответ. 10.
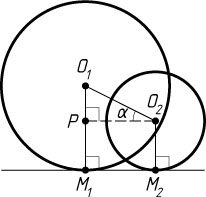
Указание. Рассмотрите прямоугольный треугольник O_{1}PO_{2}
, где P
— проекция точки O_{2}
на O_{1}M_{1}
.
Решение. Пусть P
— проекция точки O_{2}
на прямую O_{1}M_{1}
. Обозначим \angle O_{1}O_{2}P=\alpha
. Тогда
\cos\alpha=\frac{O_{2}P}{O_{1}O_{2}}=\frac{M_{1}M_{2}}{O_{1}O_{2}}=\frac{2\sqrt{5}}{5},
\sin\alpha=\frac{\sqrt{5}}{5},~\ctg\alpha=\frac{\cos\alpha}{\sin\alpha}=2.
В прямоугольном треугольнике O_{1}PO_{2}
:
O_{1}P=O_{1}M_{1}-PM_{1}=O_{1}M_{1}-O_{2}M_{2}=12-7=5,
M_{1}M_{2}=O_{2}P=O_{1}P\cdot\ctg\alpha=5\cdot2=10.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1980 (отделение политической экономии), вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 99
Источник: Вступительный экзамен в МИЭТ. — 1986, № 10
Источник: Журнал «Квант». — 1987, № 5, с. 59
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.17, с. 61
