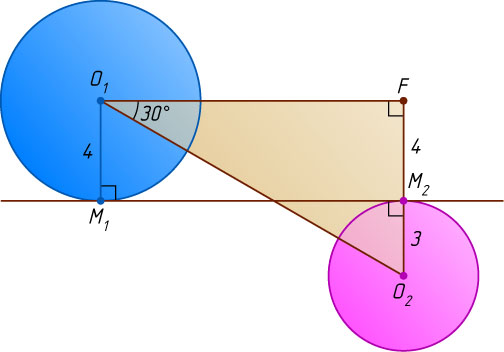
880. На плоскости даны две окружности радиусов 4 и 3 с центрами в точках O_{1}
и O_{2}
, касающиеся некоторой прямой в точках M_{1}
и M_{2}
и лежащие по разные стороны от этой прямой. Отношение отрезка O_{1}O_{2}
к отрезку M_{1}M_{2}
равно \frac{2}{\sqrt{3}}
. Найдите O_{1}O_{2}
.
Ответ. 14.
Решение. Опустим перпендикуляр O_{1}F
из центра первой окружности на продолжение радиуса O_{2}M_{2}
второй окружности. Тогда
O_{1}F=M_{1}M_{2},~M_{2}F=O_{1}M_{1}=4,~O_{2}F=O_{2}M_{2}+M_{2}F=3+4=7.
Из прямоугольного треугольника O_{1}FO_{2}
находим, что
\cos\angle FO_{1}O_{2}=\frac{O_{1}F}{O_{1}O_{2}}=\frac{M_{1}M_{2}}{O_{1}O_{2}}=\frac{\sqrt{3}}{2},
значит, \angle FO_{1}O_{2}=30^{\circ}
. Следовательно, O_{1}O_{2}=2O_{2}F=2\cdot7=14
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1980 (отделение политической экономии), вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 100
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.16, с. 61
