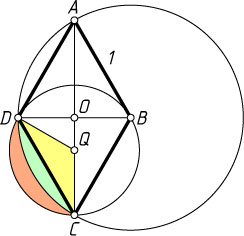
883. В параллелограмме ABCD
сторона AB
равна 1 и равна диагонали BD
. Диагонали относятся как 1:\sqrt{3}
. Найдите площадь той части круга, описанного около треугольника BCD
, которая не принадлежит кругу, описанному около треугольника ADC
.
Ответ. \frac{\sqrt{3}}{6}-\frac{\pi}{18}
.
Указание. Докажите, что AC\gt BD
, а треугольник BDC
— равносторонний.
Решение. Предположим, что AC\lt BD
. Тогда AC=\frac{\sqrt{3}}{3}
. Если O
— точка пересечения диагоналей параллелограмма ABCD
, то в треугольнике ABO
известно, что
AB=1,~OB=\frac{1}{2},~AO=\frac{\sqrt{3}}{6},
что невозможно, поскольку \frac{1}{2}+\frac{\sqrt{3}}{6}\lt1
. Следовательно, AC\gt BD
и AC=\sqrt{3}
. Тогда треугольник BDC
— равносторонний. Центр Q
окружности, описанной около этого треугольника, лежит на отрезке OC
и \frac{OC}{QO}=2
, радиус этой окружности равен \frac{\sqrt{3}}{3}
, а площадь сектора DQC
равна
\frac{1}{3}\pi\left(\frac{\sqrt{3}}{3}\right)^{2}=\frac{\pi}{9}.
Вычитая из этой площади площадь треугольника DQC
, получим \frac{\pi}{9}-\frac{\sqrt{3}}{12}
.
Центр окружности, описанной около треугольника ADC
, — точка B
; радиус этой окружности равен 1. Площадь сектора DBC
равна \frac{\pi}{6}
. Вычитая из этой площади площадь треугольника BDC
, получим \frac{\pi}{6}-\frac{\sqrt{3}}{4}
. Следовательно, искомая площадь равна
\left(\frac{\pi}{9}-\frac{\sqrt{3}}{12}\right)-\left(\frac{\pi}{6}-\frac{\sqrt{3}}{4}\right)=\frac{\sqrt{3}}{6}-\frac{\pi}{18}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1982 (отд. структурной и прикладной лингвистики), вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 126
