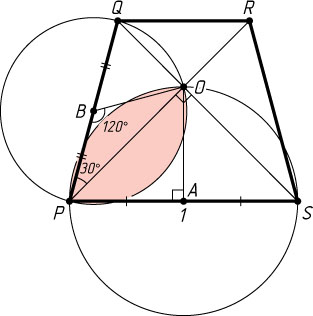
884. В равнобедренной трапеции PQRS
диагонали перпендикулярны и точкой пересечения O
делятся в отношении 1:\sqrt{3}
. Большее основание PS
трапеции равно 1. Найдите площадь общей части кругов, описанных около треугольников PQO
и POS
.
Ответ. \frac{17\pi}{144}-\frac{3+\sqrt{3}}{24}
.
Указание. Центры окружностей, описанных около треугольников PQO
и POS
, — середины отрезков PQ
и PS
.
Решение. Центр A
окружности, описанной около треугольника POS
, — середина основания PS
, радиус этой окружности равен \frac{1}{2}
. Площадь сектора OAP
равна
\frac{1}{4}\pi\left(\frac{1}{2}\right)^{2}=\frac{\pi}{16}.
Вычитая из неё площадь треугольника OAP
, получим
\frac{\pi}{16}-\frac{1}{2}\left(\frac{1}{2}\right)^{2}=\frac{\pi}{16}-\frac{1}{8}.
Поскольку
\ctg\angle OPQ=\frac{PQ}{OQ}=\frac{PO}{OR}=\sqrt{3},
то \angle OPQ=30^{\circ}
. Поэтому
PQ=\frac{PO}{\cos30^{\circ}}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{6}}.
Центр B
окружности, описанной около прямоугольного треугольника OPQ
, — середина стороны PQ
, её радиус равен \frac{1}{2}PQ=\frac{1}{\sqrt{6}}
, \angle OBP=120^{\circ}
. Площадь сектора OBP
равна
\frac{1}{3}\pi\left(\frac{1}{\sqrt{6}}\right)^{2}=\frac{\pi}{18}.
Вычитая из неё площадь треугольника OBP
, получим
\frac{\pi}{18}-\frac{1}{2}\left(\frac{1}{\sqrt{6}}\right)^{2}\frac{\sqrt{3}}{2}=\frac{\pi}{18}-\frac{\sqrt{3}}{24}.
Следовательно, искомая площадь равна
\left(\frac{\pi}{16}-\frac{1}{8}\right)+\left(\frac{\pi}{18}-\frac{\sqrt{3}}{24}\right)=\frac{17\pi}{144}-\frac{3+\sqrt{3}}{24}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1982 (отд. структурной и прикладной лингвистики), вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 126
