891. В окружность вписан равнобедренный треугольник с основанием a
и углом при основании \alpha
. Кроме того, построена вторая окружность, касающаяся первой окружности и основания треугольника, причём точка касания является серединой основания. Найдите радиус второй окружности. Если решение не единственное, рассмотрите все случаи.
Ответ. \frac{a}{4}\tg\alpha
, \frac{a}{4}\ctg\alpha
.
Указание. Диаметр одной из искомых окружностей — высота данного треугольника, а другой — разность между диаметром описанной окружности и диаметром первой искомой окружности.
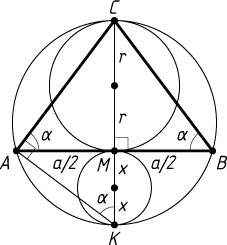
Решение. Пусть CK
— диаметр окружности, описанной около равнобедренного треугольника ABC
(AC=BC
, AB=a
, \angle A=\angle B=\alpha
). Тогда середина M
основания AB
принадлежит этому диаметру, а CM
и MK
— диаметры искомых окружностей.
Пусть r
и x
— радиусы искомых окружностей. Тогда
r=\frac{1}{2}CM=\frac{1}{2}AM\cdot\tg\alpha=\frac{a}{4}\tg\alpha,
x=\frac{1}{2}MK=\frac{1}{2}AM\cdot\ctg\angle AKM=\frac{a}{4}\ctg\alpha.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1973, № 2, вариант 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.20, с. 68
