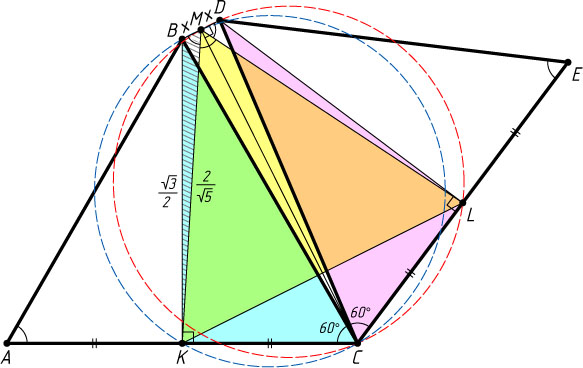
893. Два одинаковых правильных треугольника ABC
и CDE
со стороной 1 расположены так, что имеют только одну общую точку C
и угол BCD
меньше, чем 60^{\circ}
. Точка K
— середина AC
, точка L
— середина CE
, точка M
— середина BD
. Площадь треугольника KLM
равна \frac{\sqrt{3}}{5}
. Найдите BD
.
Ответ. \frac{2-\sqrt{3}}{\sqrt{5}}
.
Решение. Поскольку CM
— медиана равнобедренного треугольника BCD
, то CM
— высота этого треугольника. Отрезок CD
виден из точек M
и L
под прямым углом. Следовательно, точки D
, L
, C
и M
расположены на окружности с диаметром CD
. Поэтому
\angle DML=\angle DCL=60^{\circ}.
Аналогично \angle BMK=60^{\circ}
. Тогда \angle KML=60^{\circ}
, а так как MK=ML
(из равенства треугольников MKC
и MLC
), то треугольник KLM
— равносторонний. Поскольку его площадь равна \frac{\sqrt{3}}{5}
, то сторона равна \frac{2}{\sqrt{5}}
.
Пусть BD=2x
. Тогда, применив теорему косинусов к треугольнику BMK
, получим уравнение
x^{2}+\frac{4}{5}-\frac{2x}{\sqrt{5}}=\frac{3}{4},~\mbox{или}~x^{2}-\frac{2x}{\sqrt{5}}+\frac{1}{20}=0.
Условию задачи удовлетворяет только один корень этого уравнения:
x=\frac{2-\sqrt{3}}{2\sqrt{5}}\lt\frac{1}{2}.
Следовательно, BD=2x=\frac{2-\sqrt{3}}{\sqrt{5}}
.
Источник: Вступительный экзамен на физический факультет МГУ. — 1974, вариант 1, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 205
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 224, с. 26
