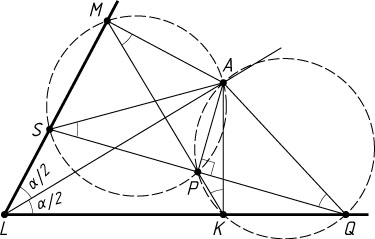
896. На биссектрисе угла с вершиной L
взята точка A
. Точки K
и M
— основания перпендикуляров, опущенных из точки A
на стороны угла. На отрезке KM
взята точка P
(KP\lt PM
) и через точку P
перпендикулярно к отрезку AP
проведена прямая, пересекающая прямую KL
в точке Q
(K
между Q
и L
), а прямую ML
— в точке S
. Известно, что \angle KLM=\alpha
, KM=a
, QS=b
. Найдите KQ
.
Ответ. \frac{\sqrt{b^{2}-a^{2}}}{2\cos\frac{\alpha}{2}}
.
Указание. Точки P
, K
, Q
и A
лежат на одной окружности.
Решение. Поскольку \angle AKQ=\angle APQ=90^{\circ}
, то точки P
, K
, Q
и A
лежат на окружности с диаметром AQ
. Следовательно,
\angle AQS=\angle AKM=\angle ALK=\frac{\alpha}{2}.
Аналогично \angle ASQ=\frac{\alpha}{2}
. Поэтому треугольник QAS
— равнобедренный. Тогда
AQ=\frac{QP}{\cos\frac{\alpha}{2}}=\frac{\frac{b}{2}}{\cos\frac{\alpha}{2}}.
Из равнобедренного треугольника AKM
находим, что
AK=\frac{\frac{1}{2}KM}{\cos\frac{\alpha}{2}}=\frac{\frac{a}{2}}{\cos\frac{\alpha}{2}}.
По теореме Пифагора из прямоугольного треугольника AKQ
находим, что
KQ=\sqrt{AQ^{2}-AK^{2}}=\frac{\sqrt{b^{2}-a^{2}}}{2\cos\frac{\alpha}{2}}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1974, вариант 4, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 206
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.35, с. 106
