900. Дан прямоугольный треугольник ABC
с прямым углом при вершине C
. Угол CAB
равен \alpha
. Биссектриса угла ABC
пересекает катет AC
в точке K
. На стороне BC
как на диаметре построена окружность, которая пересекает гипотенузу AB
в точке M
. Найдите угол AMK
.
Ответ. \arctg\frac{1}{\cos\alpha}
.
Указание. Пусть F
и P
— проекции точки K
на AB
и CM
. Тогда KF=KC
и KP=FM
.
Решение. Угол CMB
вписан в данную окружность и опирается на её диаметр. Поэтому угол CMB
— прямой. Опустим из точки K
перпендикуляры KF
и KP
на прямые AB
и CM
соответственно. Тогда
\tg\angle AMK=\frac{KF}{FM}=\frac{KC}{KP}=\frac{1}{\cos\angle CKP}=\frac{1}{\cos\alpha}
(так как KF=KC
, а FM=KP
).
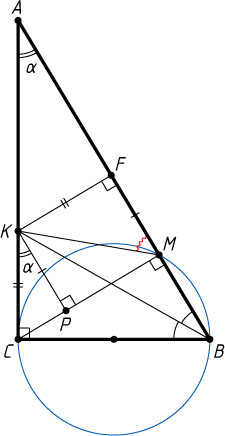
Источник: Вступительный экзамен на геологический факультет МГУ. — 1974, вариант 1, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 133
