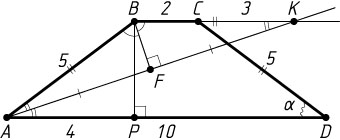
901. Дана равнобедренная трапеция ABCD
. Известно, что AD=10
, BC=2
, AB=CD=5
. Биссектриса угла BAD
пересекает продолжение основания BC
в точке K
. Найдите биссектрису угла ABK
в треугольнике ABK
.
Ответ. \frac{\sqrt{10}}{2}
.
Указание. Треугольник ABK
— равнобедренный.
Решение. Пусть \angle BAD=\alpha
. Поскольку
\angle BKA=\angle KAD=\angle BAK,
то треугольник ABK
— равнобедренный, BK=AB=5
. Его биссектриса BF
является высотой. Следовательно,
BF=AB\sin\angle BAF=5\sin\frac{\alpha}{2}.
Пусть P
— проекция точки B
на AD
. Тогда
AP=\frac{AD-BC}{2}=4,~\cos\alpha=\cos\angle BAD=\frac{AP}{AB}=\frac{4}{5}.
Поэтому
\sin\frac{\alpha}{2}=\sqrt{\frac{1-\cos\alpha}{2}}=\frac{1}{\sqrt{10}}.
Следовательно,
BF=5\sin\frac{\alpha}{2}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1974 (отделение общей геологии), вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 134
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5.27, с. 50
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.27.1, с. 50
