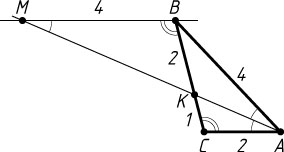
902. Дан треугольник ABC
. Известно, что AB=4
, AC=2
и BC=3
. Биссектриса угла BAC
пересекает сторону BC
в точке K
. Прямая, проходящая через точку B
параллельно AC
, пересекает продолжение биссектрисы AK
в точке M
. Найдите KM
.
Ответ. 2\sqrt{6}
.
Указание. Треугольник ABM
— равнобедренный.
Решение. По теореме косинусов из треугольника ABC
находим, что
\cos\angle C=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{4+9-16}{2\cdot2\cdot3}=-\frac{1}{4}.
По свойству биссектрисы треугольника
\frac{BK}{KC}=\frac{AB}{AC}=\frac{4}{2}=2.
Поэтому BK=2
.
Поскольку
\angle AMB=\angle CAM=\angle MAB,
то треугольник ABM
— равнобедренный, BM=AB=4
. Кроме того,
\angle KBM=\angle KCA=\angle C.
Следовательно,
KM^{2}=BK^{2}+BM^{2}-2BK\cdot BM\cos\angle KBM=4+16-2\cdot2\cdot4\cdot\left(-\frac{1}{4}\right)=24.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1974, вариант 3, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 133
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 127, с. 16
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.16, с. 47
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.27.2, с. 50
