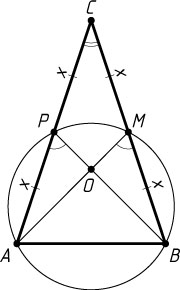
904. Дан треугольник ABC
. Из вершины A
проведена медиана AM
, а из вершины B
— медиана BP
. Известно, что угол APB
равен углу BMA
. Косинус угла ACB
равен 0,8 и BP=1
. Найдите площадь треугольника ABC
.
Ответ. \frac{2}{3}
.
Указание. Точки A
, B
, M
и P
лежат на одной окружности. Треугольник ABC
— равнобедренный.
Решение. Первый способ. Поскольку \angle APB=\angle BMA
, то точки A
, B
, M
, и P
лежат на одной окружности; CB
и CA
— секущие, поэтому CM\cdot CB=CP\cdot CA
, или 2CM^{2}=2CP^{2}
. Следовательно, CM=CP
, поэтому CA=CB
, т. е. треугольник ABC
— равнобедренный.
Пусть MC=x
. Тогда AC=2x
. По теореме косинусов
AM^{2}=CM^{2}+AC^{2}-2CM\cdot AC\cos\angle ACB,~\mbox{или}
1=x^{2}+4x^{2}-2x\cdot2x\cdot\frac{4}{5}.
Откуда находим, что x^{2}=\frac{5}{9}
. Тогда
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\sin\angle C=\frac{1}{2}\cdot(2x)^{2}\cdot\frac{3}{5}=
=\frac{6x^{2}}{5}=\frac{6}{5}\cdot\frac{5}{9}=\frac{2}{3}.
Второй способ. Пусть O
— точка пересечения медиан треугольника ABC
. Треугольники AOP
и BOM
подобны (по двум углам). Поэтому AO:OB=PO:OM
. Следовательно, AO\cdot OM=BO\cdot OP
, или \frac{2}{9}AM^{2}=\frac{2}{9}BP^{2}
(так как медианы делятся точкой пересечения в отношении 2:1
, считая от вершины треугольника). Поэтому AM=BP
. Следовательно, треугольник ABC
— равнобедренный. Далее см. первый способ.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1974, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 141
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.29, с. 105
