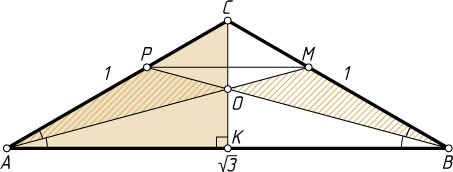
905. В треугольнике ABC
биссектриса угла при вершине A
пересекает сторону BC
в точке M
, а биссектриса угла при вершине B
пересекает сторону AC
в точке P
. Биссектрисы AM
и BP
пересекаются в точке O
. Известно, что треугольник BOM
подобен треугольнику AOP
, BO=(1+\sqrt{3})OP
, BC=1
. Найдите площадь треугольника ABC
.
Ответ. \frac{\sqrt{3}}{4}
.
Указание. Докажите, что треугольник ABC
— равнобедренный.
Решение. Из подобия треугольников BOM
и AOP
следует равенство углов MBP
и MAP
. Поэтому
\angle ABC=2\angle MBP=2\angle MAP=\angle BAC.
Следовательно, треугольник ABC
— равнобедренный. Тогда MP\parallel AB
. По свойству биссектрисы треугольника \frac{AB}{AC}=\frac{BM}{MC}
. Поскольку
\frac{CM}{CB}=\frac{PM}{AB}=\frac{OP}{OB}=\frac{1}{1+\sqrt{3}},
то \frac{BM}{MC}=\sqrt{3}
. Следовательно, \frac{AB}{AC}=\sqrt{3}
. Отсюда находим, что
AB=AC\sqrt{3}=BC\sqrt{3}=\sqrt{3}.
Найдём теперь высоту CK
равнобедренного треугольника ABC
:
CK=\sqrt{AC^{2}-AK^{2}}=\sqrt{1-\frac{3}{4}}=\frac{1}{2}.
Следовательно, S_{\triangle ABC}=\frac{\sqrt{3}}{4}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1974 (отделение геофизики), вариант 2, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 141
