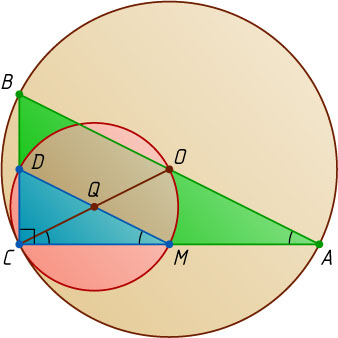
909. В прямоугольном треугольнике ABC
угол C
— прямой, а сторона CA=4
. На катете BC
взята точка D
, причём CD=1
. Окружность радиуса \frac{\sqrt{5}}{2}
проходит через точки C
и D
и касается в точке C
окружности, описанной около треугольника ABC
. Найдите площадь треугольника ABC
.
Ответ. 4.
Указание. Докажите, что окружности касаются внутренним образом. Если M
— отличная от C
точка пересечения первой окружности с катетом AC
, то треугольники MCD
и ACB
подобны.
Решение. Поскольку точка D
лежит внутри окружности, описанной около треугольника ABC
, то данные окружности касаются внутренним образом. Если M
— отличная от C
точка пересечения первой окружности с катетом AC
, то MD
— диаметр этой окружности,
MC=\sqrt{MD^{2}-CD^{2}}=\sqrt{5-1}=2.
Пусть Q
и O
— середины диаметров MD
и AB
данных окружностей. Тогда точки O
, Q
и C
лежат на одной прямой, треугольники MQC
и AOC
— равнобедренные, \angle CMD=\angle ACO=\angle BAC
, поэтому треугольники MCD
и ACB
подобны с коэффициентом \frac{MC}{CA}=\frac{1}{2}
. Следовательно,
BC=2CD=2,~S_{\triangle ABC}=\frac{1}{2}BC\cdot AC=4.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1974, вариант 2, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 87
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 3, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 166
