916. Два равных равнобедренных треугольника ABC
и DBE
(AB=BC=DB=BE
) имеют общую вершину B
и лежат в одной плоскости, причём точки A
и C
находятся по разные стороны от прямой BD
, а отрезки AC
и DE
пересекаются в точке K
. Известно, что \angle ABC=\angle DBE=\alpha\lt\frac{\pi}{2}
, \angle AKD=\beta\lt\alpha
. В каком отношении прямая BK
делит угол ABC
?
Ответ. \frac{\alpha+\beta}{\alpha-\beta}
.
Указание. \angle ABD=\angle CBE=\beta
Решение. Поскольку
\angle ABD=\angle ABC-\angle DBC,~\angle CBE=\angle DBE-\angle DBC,~\angle ABC=\angle DBE,
то \angle ABD=\angle CBE
. Точки A
, D
, C
, E
лежат на окружности с центром в точке B
и радиусом, равным AB
. Поэтому \angle DAK=\angle CEK
.
Отрезок BK
виден из точек A
и D
под одним углом (\angle BAK=\angle BDK
). Поэтому точки A
, D
, K
и B
расположены на одной окружности. Следовательно, \angle DBK=\angle DAK
. Аналогично докажем, что \angle CBK=\angle CEK
. Поэтому
\angle ABK=\angle ABD+\angle DBK=\beta+\frac{\alpha-\beta}{2}=\frac{\alpha+\beta}{2},~\angle KBC=\frac{1}{2}\angle DBC=\frac{\alpha-\beta}{2}.
Следовательно,
\frac{\angle ABK}{\angle KBC}=\frac{\alpha+\beta}{\alpha-\beta}.
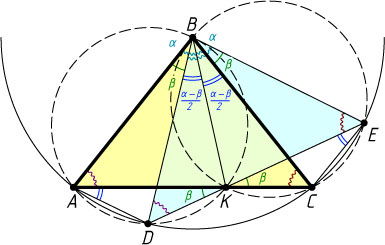
Источник: Вступительный экзамен на механико-математический факультет МГУ. — № 3, 1975, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 283
