920. Дана прямоугольная трапеция, основания которой равны a
и b
(a\lt b
). Известно, что некоторая прямая, параллельная основаниям, рассекает её на две трапеции, в каждую из которых можно вписать окружность. Найдите радиусы этих окружностей.
Ответ. \frac{a\sqrt{b}}{\sqrt{a}+\sqrt{b}}
, \frac{b\sqrt{a}}{\sqrt{a}+\sqrt{b}}
.
Указание. Докажите, что указанная прямая разбивает данную трапецию на две подобных трапеции.
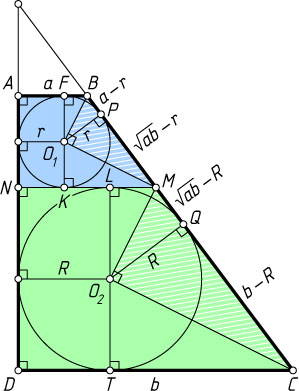
Решение. Пусть AB=a
и CD=b
— основания трапеции, M
и N
— точки пересечения указанной прямой с боковыми сторонами BC
и AD
, O_{1}
и O_{2}
— центры окружностей, вписанных в трапеции ABMN
и NMCD
, r
и R
— радиусы этих окружностей, P
и Q
— точки касания окружностей с большей боковой стороной BC
, K
и L
— с отрезком MN
, F
и T
— с основаниями AB
и CD
соответственно.
При гомотетии с центром в точке пересечения прямых CB
и DA
и коэффициентом \frac{R}{r}
меньшая окружность переходит в большую, а трапеция ABMN
— в трапецию NMCD
. Следовательно, эти трапеции подобны. Поэтому \frac{AB}{MN}=\frac{MN}{CD}
. Отсюда находим, что MN=\sqrt{ab}
. Тогда
PM=MK=MN-KN=\sqrt{ab}-r,~BP=BF=BA-AF=a-r.
В прямоугольном треугольнике BO_{1}M
O_{1}P^{2}=BP\cdot PM,~\mbox{или}~r^{2}=(a-r)(\sqrt{ab}-r).
Отсюда находим, что r=\frac{a\sqrt{b}}{\sqrt{a}+\sqrt{b}}
. Аналогично R=\frac{b\sqrt{a}}{\sqrt{a}+\sqrt{b}}
.
