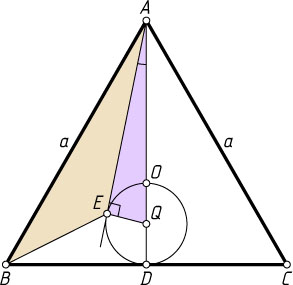
926. В правильном треугольнике ABC
проведена окружность, проходящая через центр треугольника и касающаяся стороны BC
в её середине D
. Из точки A
проведена прямая, касающаяся окружности в точке E
, причём \angle BAE\lt30^{\circ}
. Найдите площадь треугольника ABE
, если площадь треугольника ABC
равна \frac{10}{4-\sqrt{2}}
.
Ответ. 1.
Указание. Найдите \sin\angle DAE
из прямоугольного треугольника EAQ
(Q
— центр данной окружности).
Решение. Пусть O
— центр треугольника ABC
, Q
— центр данной окружности. Обозначим через a
сторону треугольника ABC
. Тогда
OD=\frac{1}{3}AD=\frac{a\sqrt{3}}{6},~OQ=QD=\frac{a\sqrt{3}}{12},
AQ=AD-QD=\frac{a\sqrt{3}}{2}-\frac{a\sqrt{3}}{12}=\frac{5a\sqrt{3}}{12}.
Из прямоугольного треугольника AEQ
находим, что
\sin\angle EAQ=\frac{EQ}{AQ}=\frac{1}{5},~\cos\angle EAQ=\frac{2\sqrt{6}}{5},
AE=EQ\tg\angle EAQ=\frac{a\sqrt{2}}{2}.
Следовательно,
S_{\triangle ABE}=\frac{1}{2}AE\cdot AB\sin(30^{\circ}-\angle EAQ)=
=\frac{a^{2}}{\sqrt{2}}\cdot\frac{\frac{\sqrt{6}}{5}-\frac{\sqrt{3}}{15}}{4}=\frac{a^{2}\sqrt{6}(2\sqrt{2}-1)}{40}.
По условию задачи
S_{\triangle ABC}=\frac{10}{4-\sqrt{2}}=\frac{a^{2}\sqrt{3}}{4}.
Выразим из этого равенства a^{2}
и подставим в предыдущее. Получим: S_{\triangle ABE}=1
Источник: Вступительный экзамен на геологический факультет МГУ. — 1975 (отделение общей геологии), вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 148
