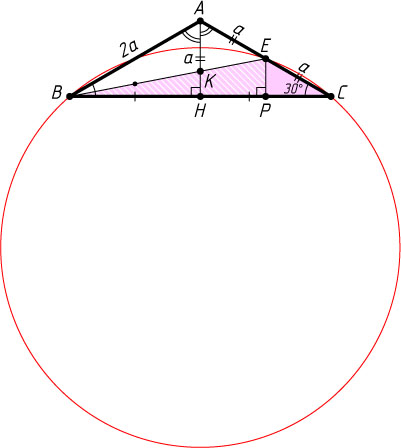
930. В треугольнике ABC
биссектриса AH
делит медиану BE
в отношении BK:KE=2
, а угол ACB
равен 30^{\circ}
. Найдите отношение площади треугольника BCE
к площади описанного около этого треугольника круга.
Ответ. \frac{\sqrt{3}}{14\pi}
.
Указание. Треугольник ABC
— равнобедренный.
Решение. Медианы треугольника делятся их точкой пересечения в отношении 2:1
, считая от вершины треугольника. Поэтому K
— точка пересечения медиан треугольника ABC
. Следовательно, AH
— медиана треугольника ABC
. Поэтому треугольник ABC
— равнобедренный.
Обозначим AB=AC=2a
. Тогда AH=AB\sin30^{\circ}=a
. Если P
— проекция точки E
на BC
, то
EP=\frac{1}{2}AH=\frac{a}{2},~BP=BH+HP=BH+\frac{1}{2}BH=\frac{3}{2}BH=\frac{3a\sqrt{3}}{2},
BE^{2}=BP^{2}+PE^{2}=\frac{27a^{2}}{4}+\frac{a^{2}}{4}=7a^{2},~BE=a\sqrt{7}.
Если R
— радиус описанной окружности треугольника BCE
, то
R=\frac{BE}{2\sin\angle ECB}=\frac{BE}{2\sin30^{\circ}}=BE=a\sqrt{7}.
Поэтому площадь круга, описанного около треугольника BCE
равна 7\pi a^{2}
.
Поскольку
S_{\triangle BCE}=\frac{1}{2}BC\cdot PE=\frac{a^{2}\sqrt{3}}{2},
то искомое отношение равно \frac{\sqrt{3}}{14\pi}
.
Источник: Вступительный экзамен на географический факультет МГУ. — 1975, вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 64
