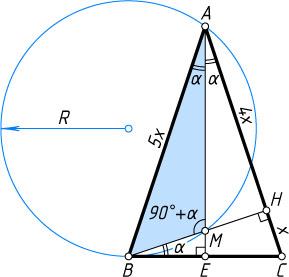
931. В треугольнике ABC
высота BH
делит сторону AC
в отношении AH:HC=4
, а угол HBC
вдвое меньше угла BAC
. Биссектриса AE
угла BAC
пересекается с BH
в точке M
. Найдите отношение площади треугольника ABM
к площади описанного около этого треугольника круга.
Ответ. \frac{12}{25\pi}
.
Указание. Докажите, что треугольник ABM
— равнобедренный и найдите \cos\angle BAC
.
Решение. Обозначим \angle HBC=\alpha
. Тогда \angle BAM=\angle CAM=\alpha
. Поскольку \angle BME=\angle AMH
, то
\angle BEM=\angle AHM=90^{\circ},
т. е. биссектриса AE
треугольника ABC
является его высотой. Тогда треугольник ABC
— равнобедренный.
Обозначим CH=x
. Тогда
AH=4x,~AB=AC=5x,~\cos2\alpha=\cos\angle BAC=\frac{AH}{AB}=\frac{4}{5},
\cos\alpha=\frac{3}{\sqrt{10}}.
Поскольку
\angle BMA=\angle AHB+\angle MAH=90^{\circ}+\alpha,
то
R=\frac{AB}{2\sin\angle BMA}=\frac{5x}{2\cos\alpha}=\frac{5x\sqrt{10}}{6},
где R
— радиус окружности, описанной около треугольника ABM
.
По теореме Пифагора из треугольника ABH
находим, что
BH=\sqrt{25x^{2}-16x^{2}}=3x.
Поэтому
S_{\triangle ABH}=\frac{1}{2}4x\cdot3x=6x^{2}.
По свойству биссектрисы треугольника \frac{BM}{MH}=\frac{5}{4}
. Следовательно,
S_{\triangle ABM}=\frac{5}{9}S_{\triangle ABH}=\frac{10x^{2}}{3}.
Тогда искомое отношение равно
\frac{\frac{10x^{2}}{3}}{\frac{25x^{2}\cdot10\pi}{36}}=\frac{12}{25\pi}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1975, вариант 3, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 65
