933. В прямоугольной трапеции меньшее основание равно высоте, а большее основание равно a
. Найдите боковые стороны трапеции, если известно, что одна из них касается окружности, проходящей через концы меньшего основания и касающейся большего основания.
Ответ. \frac{4a}{7}
, \frac{5a}{7}
.
Указание. Точка касания данной окружности с нижнем основанием лежит на серединном перпендикуляре к верхнему основанию.
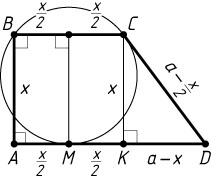
Решение. Обозначим меньшее основание BC
и меньшую боковую сторону трапеции ABCD
через x
. Пусть M
— точка касания окружности с большим основанием AD
. Тогда точка M
лежит на серединном перпендикуляре к отрезку BC
, поэтому
AM=\frac{1}{2}BC=\frac{x}{2},~CD=MD=AD-AM=a-\frac{x}{2}.
Пусть K
— проекция вершины C
на AD
. Тогда KD=a-x
, CK=x
. По теореме Пифагора
CD^{2}=CK^{2}+KD^{2},~\mbox{или}~\left(a-\frac{x}{2}\right)^{2}=x^{2}+(a-x)^{2}.
Отсюда находим, что x=\frac{4a}{7}
. Тогда
CD=a-\frac{x}{2}=a-\frac{2a}{7}=\frac{5a}{7}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1975, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.19, с. 61
