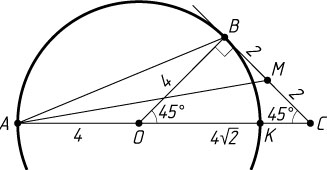
935. В окружности радиуса R=4
проведены хорда AB
и диаметр AK
, образующий с хордой угол \frac{\pi}{8}
. В точке B
проведена касательная к окружности, пересекающая продолжение диаметра AK
в точке C
. Найдите медиану AM
треугольника ABC
.
Ответ. 2\sqrt{9+6\sqrt{2}}
.
Указание. Пусть O
— центр окружности. Тогда OBC
— равнобедренный прямоугольный треугольник.
Решение. Пусть O
— центр окружности. Тогда
\angle BOC=2\angle BAO=45^{\circ}.
Из прямоугольного треугольника OBC
находим, что BC=4
и OC=4\sqrt{2}
. Поэтому AC=AO+OC=4+4\sqrt{2}
. Медиану AM
находим по теореме косинусов из треугольника AMC
:
AM^{2}=AC^{2}+CM^{2}-2AC\cdot CM\cos45^{\circ}=
=(4+4\sqrt{2})^{2}+4-2\cdot2\cdot(4+4\sqrt{2})\cdot\frac{\sqrt{2}}{2}=4(9+6\sqrt{2}).
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1986, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 26
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.25, с. 62
