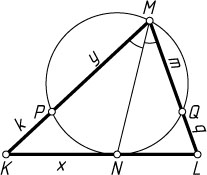
941. В треугольнике KLM
проведена биссектриса MN
. Через вершину M
проходит окружность, касающаяся стороны KL
в точке N
и пересекающая сторону KM
в точке P
, а сторону LM
— в точке Q
. Отрезки KP
, QM
и LQ
соответственно равны k
, m
и q
. Найдите MN
.
Ответ. \sqrt{\frac{km(m+q)}{q}}
.
Указание. Примените формулу для биссектрисы треугольника:
MN^{2}=KM\cdot LM-KN\cdot LN.
Решение. Обозначим KN=x
, PM=y
. По теореме о касательной к секущей
NL^{2}=LQ\cdot LM=q(m+q),~KN^{2}=KP(KP+PM),~\mbox{или}~x^{2}=k(k+y).
Кроме того, по свойству биссектрисы треугольника
\frac{KM}{KN}=\frac{LM}{LN},~\mbox{или}~\frac{k+y}{x}=\frac{m+q}{\sqrt{q(m+q)}}=\frac{\sqrt{m+q}}{\sqrt{q}}.
Из полученной системы находим, что
k+y=\frac{k(m+q)}{q},~x=\frac{k\sqrt{m+q}}{\sqrt{q}}.
По формуле для биссектрисы треугольника (см. задачу 791)
MN^{2}=KM\cdot LM-KN\cdot LN=(k+y)(m+q)-x\sqrt{q(m+q)}=\frac{km(m+q)}{q}.